Lean 4 Mathematical Formal Proofs Propel the Next Leap in AI Reasoning After o1
1. Introduction
The OpenAI o1 model has garnered immense attention due to its exceptional reasoning capabilities. In terms of reasoning and thinking abilities, o1 surpasses previous models, particularly in tasks such as Science and Coding. Its outstanding performance in handling complex tasks has sparked in-depth discussions on the reasoning capabilities of models. Furthermore, with the continuous advancement of technology, many fields now rely on sophisticated mathematical algorithms and precise logical reasoning. For instance, in areas such as finance, engineering, physics, and computer science, the complexity and scale of problems are constantly increasing. How to enhance AI's reasoning abilities has become an urgent challenge that needs to be addressed.
2. The Frontier of Reasoning Capabilities: Mathematical Formal Proofs
2.1 Why We Need Model Reasoning Capabilities
Mathematics and logical reasoning serve as the foundation of science and engineering, playing a critical role in solving complex problems. Large models, with enhanced reasoning capabilities, can better simulate human problem-solving approaches, thereby providing deeper insights and more accurate decision-making support in fields such as scientific research, engineering design, medical diagnosis, and financial analysis. Additionally, with the explosive growth of data, we need more intelligent systems to process and analyze this data. Large models equipped with reasoning capabilities are key tools to achieve this goal. We expect models to:
- Solve Complex Problems: The complexity of modern scientific and engineering problems exceeds the capacity of traditional methods. The introduction of large models enables the handling and resolution of these complex issues.
- Improve Efficiency and Accuracy: By automating reasoning and computation, large models can significantly enhance the efficiency of complex tasks and reduce human errors.
- Drive Innovation and Discovery: Leveraging their powerful reasoning abilities, large models can explore and innovate in uncharted territories, uncovering new theories and principles.
OpenAI's o1, with its demonstrated reasoning capabilities in complex tasks, has ignited a wave of research and development in model reasoning across the industry. However, how to further enhance this capability has become a challenge for AI researchers. Integrating formal verification into the training of large AI models is undoubtedly an effective path to elevate their reasoning abilities.
2.2 What is Formal Proof
In the construction of mathematical systems, proofs hold an indispensable position. The fundamental task of mathematical research is to explore the properties, relationships, and structures of mathematical objects, all of which rely on rigorous logical reasoning. In mathematics, proofs are not merely a presentation of results; in the context of modern mathematics, proofs serve as the core of mathematical research, fulfilling dual roles of exploration and verification. As research objects grow in complexity and theoretical systems expand, the demand for proof rigor has significantly increased. Traditional informal proofs, while historically impactful, often fail to meet the requirements of rigor and accuracy when faced with increasingly complex mathematical concepts. Formal proofs, compared to informal proofs, offer the following advantages:
- Precision and Reliability: Formal proofs avoid ambiguity through strict logic and explicit expression, ensuring the precision and reliability of the reasoning process.
- Systematic Verification: Formal proofs provide a systematic method to verify the correctness of mathematical propositions using axioms, theorems, and inference rules.
- Transparency and Reproducibility: Individuals with relevant background knowledge can independently review and verify each step of formal proofs, ensuring the correctness and reproducibility of mathematical theories.
The core of formal proofs lies in the use of rigorous axiomatic systems, theorems, and inference rules to ensure the rigor and accuracy of each reasoning step. Formal proofs offer mathematicians a precise expressive tool, enabling every logical inference to be conducted within a recognized framework, where each concept and operation is clearly defined. For example, formal axiomatic systems can strictly define various mathematical objects and their relationships.
Moreover, formal proofs promote transparency and trust within the mathematical community, facilitating the dissemination and transmission of knowledge. By using consistent logical language and symbols, researchers can establish connections across different mathematical fields and applications, making the promotion and application of theories more seamless. This transparency not only addresses the demand for proof rigor but also drives mathematical research to higher levels of development.
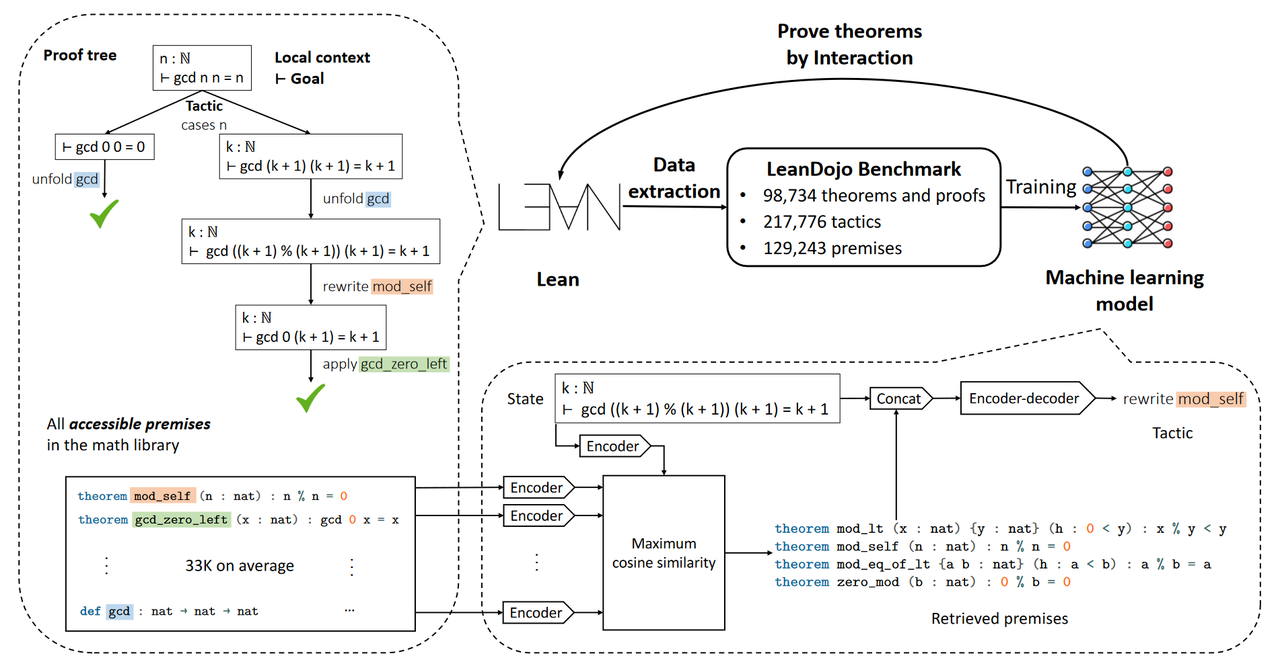
3. Lean 4: A Powerful Tool for Mathematical Formal Proofs
Lean is a programming language that serves as an auxiliary proof tool for theorem proving. It provides a rigorous logical and mathematical framework, supporting higher-order logic and dependent type theory, enabling users to perform precise reasoning and proofs efficiently. Its interactive proof environment allows users to construct proofs step-by-step and verify their correctness in real-time. The instant feedback it offers significantly reduces debugging costs for users. Additionally, Lean supports modular programming, allowing users to organize proofs and definitions into modules, facilitating reuse and management, and making the development of large-scale projects more efficient and clear.
In summary, Lean provides researchers with a reliable tool for verifying the validity of new theories and results, ensuring rigor and reproducibility throughout the research process. This integrated formal proof tool offers new perspectives for the academic community, driving higher levels of mathematical and scientific discovery.
4. What We Are Doing
The team at Abaka AI is leveraging the capabilities of Lean 4 to build a formal proof mathematical corpus, providing high-quality datasets for training reasoning models in the field of mathematical reasoning. We believe this is an endeavor of immense value and potential, both now and in the future.
4.1 Challenges in Building Lean 4 Datasets
When dealing with propositions expressed in natural language within the fields of mathematics and science, Lean 4 faces significant challenges. These propositions are often vague, lack precision, or contain implicit assumptions, making them difficult to directly translate into formal proofs. In natural language, propositions may use quantifiers such as "all," "some," or "most," which have specific meanings in mathematics but can be ambiguous in natural language contexts. This ambiguity implies many unstated assumptions and conditions, requiring additional definitions and constraints, thereby complicating logical reasoning.
Interpreting such propositions often relies on precise extraction of contextual or domain-specific knowledge to ensure all definitions and implicit assumptions are explicitly stated. Additionally, Lean 4 cannot directly identify the proof target for propositions that are not clearly stated. For example, questions like "What is the limit of this sequence?" lack a clear definition of the sequence and relevant contextual information, conflicting with Lean 4's requirement for precision and closure. Therefore, to enable Lean 4 to process such problems, they must first be transformed into concrete statements with all relevant conditions and definitions explicitly stated.
The mathematical and scientific propositions handled by Lean 4 often involve highly specialized domains, meaning even seasoned mathematicians may struggle to formalize proofs for every proposition. The specialized nature of mathematical work means a researcher may excel in one area but have limited knowledge in others. Thus, ensuring the participation of experts from various fields is crucial when building Lean 4 datasets.
The complexity of process management and reliance on participants' initiative pose significant challenges in constructing Lean 4 datasets. In large-scale data production, we cannot assume that everyone will maintain an efficient work ethic or rigorous attention to detail. Additionally, limited review mechanisms create opportunities for gaming the system.
Effective process management is essential but particularly complex to achieve. Building large-scale datasets requires collaboration across multiple individuals and steps, with each stage potentially introducing issues that reduce overall efficiency and data quality. For instance, some participants may produce low-quality data due to lack of diligence or inadequate review, negatively impacting Lean 4's reasoning and proof capabilities and potentially causing issues in subsequent research and applications.
4.2 Our Solutions
We have established collaborations with experts in mathematics and science from various universities, forming interdisciplinary teams and creating an expert database covering various branches of mathematics and related scientific fields. This enables rapid matching of project needs with domain experts for proposition parsing and proof work. A team of professional mathematicians sets strict standards for parsing natural language propositions, identifying ambiguous terms, and clarifying all definitions, symbols, and implicit assumptions. We have developed standardized interpretations for common quantifiers (e.g., "all," "some," "most") and use advanced collaborative tools to manage task allocation, progress tracking, and communication. We collect participant feedback in real-time, adjust processes and strategies, and continuously optimize our approach. An instant feedback mechanism ensures that parsed propositions undergo rigorous review by the advisory team.
To address the need for domain-specific knowledge, our solution relies not only on internal knowledge systems but also on precise collaborations with universities to utilize external expert resources, ensuring dataset quality. In selecting problems and propositions, we employ a stringent curation process to ensure each problem aligns with Lean 4's capabilities. Selected problems must exhibit logical clarity and closure while holding significant research and verification value in mathematics and science. We implement a multi-tiered evaluation process, where internal experts assess problems for academic value, technical difficulty, and suitability for Lean 4. We have designed a difficulty assessment system to classify the complexity of each proposition's proof. Based on clients' model training needs, we provide customized datasets balanced across beginner, intermediate, and advanced difficulty levels, ensuring comprehensive coverage within specified domains to enhance model performance.
We have developed a comprehensive management and quality control plan. Data production personnel must pass a series of professional certifications and assessments, including evaluations of mathematical fundamentals, Lean 4 proficiency, and data processing experience. An automated task allocation system dynamically assigns tasks based on participants' qualifications and experience to ensure efficient execution. A responsibility tracking system monitors the quality of each data producer's work, identifies potential inefficiencies, and provides real-time feedback for improvement, ensuring consistent high-quality dataset production.
4.3 How We Use Lean 4 for Mathematical Annotation
Abaka AI's high-level annotation team uses precise mathematical symbols and expressions, adhering to Lean 4's language rules, to annotate mathematical propositions, transforming them into a format recognizable by Lean 4. We strictly follow axiomatic systems, theorems, and inference rules to ensure the rigor and accuracy of each step in formal proofs.
Our workflow includes the following steps:
- Selection and Analysis of Mathematical Propositions: We select representative and challenging propositions from a wide range of mathematical fields for in-depth analysis. During screening, the team evaluates not only the logical rigor of propositions but also their relevance to clients' model needs, ensuring appropriate knowledge coverage and difficulty levels for training purposes.
- Construction of Formal Proofs: The team adds detailed annotations to mathematical symbols and expressions according to Lean 4 rules, ensuring each step of the formalization process is recognizable in Lean 4 and enhancing the clarity and rigor of reasoning.
- Dataset Organization and Optimization: We organize these formal proofs into datasets, ensuring consistency in structure, format, and symbol usage for ease of model training. Through process management and quality review, we optimize and validate the datasets to ensure their quality and usability.
- Dataset Application and Feedback: Our datasets are used to train various reasoning models. We maintain close contact with data users, collecting feedback on model performance in real-world applications. This feedback informs rapid adjustments to the datasets, optimizing proof structures, difficulty ranges, and knowledge coverage to maintain their leading edge. Based on industry needs and model feedback, we regularly update and expand the datasets to cover more domains, providing comprehensive training data for models.
4.4 Advantages of Integer's Mathematical Dataset Solutions
Compared to other datasets on the market, Abaka AI's mathematical datasets offer the following advantages:
- Extensive Coverage of Mathematical Branches: Our datasets cover multiple branches of mathematics, including but not limited to algebra, geometry, number theory, and analysis, enabling them to address mathematical problems across a wide range of scenarios.
- Diverse Problem Types and Application Scenarios: Our datasets include not only standardized mathematical propositions but also non-standard problems from real-life and application scenarios, such as mathematical reasoning tasks in everyday contexts and applied problems expressed in natural language. These span practical scenarios like financial calculations and engineering applications, helping models better understand the specific requirements of mathematics in different contexts and improving their performance in cross-domain applications.
- Richness in Advanced Logical Structures: Our datasets incorporate a wealth of advanced logical structures, such as nested reasoning, multi-step proofs, and conditional analysis. These structures more closely reflect the essence of mathematical proof processes. Each step of reasoning in the dataset is meticulously designed and annotated, ensuring that models can clearly grasp every logical step during training. By systematically understanding and applying these logical structures, models can demonstrate stronger logical rigor and efficiency when handling complex proof tasks.
- Guaranteed Data Quality and Expertise: Compared to other datasets on the market, our datasets excel in the depth of mathematical knowledge and data standardization. Based on clients' diverse needs, our datasets can be flexibly customized in terms of problem types, difficulty levels, and domain coverage, ensuring precise alignment with specific application requirements. This helps clients achieve better results in high-precision, widely applicable model applications.
5. Reflections of Molordata
Mathematics has a long history in the development of human civilization and plays an irreplaceable core role. It is not only a language for exploring the essence of the world but also a foundational science supporting the development of multiple disciplines. By revealing and exploring the abstract laws and logical structures hidden behind worldly phenomena, mathematics provides both the language and tools to describe reality and ensures the correctness and self-consistency of various scientific theories through its rigorous reasoning and precise expression, showcasing its unique power and broad application value.
The definition of mathematics has evolved over time, reflecting the expansion of research content and the deepening of understanding. In ancient civilizations, mathematics primarily focused on quantity (arithmetic) and space (geometry), applied in fields such as astronomy, agriculture, and architecture. During this period, mathematics evolved from simple calculations to theorem derivation.
In the modern era (17th to 19th centuries), mathematics became more abstract and systematic, no longer limited to solving specific problems. Algebra began exploring deeper structures, and the invention of calculus made it possible to study change. This phase marked the transition of mathematics toward high abstraction and logic, forming multiple interconnected yet independently developing fields.
In the contemporary era, especially since the 20th century, mathematics has further abstracted and systematized, finding widespread applications across various fields. Set theory became one of the foundations of modern mathematics, facilitating the formal treatment of mathematical objects. At the same time, different branches of mathematics have shown greater intrinsic unity, enabling deeper and more systematic research into abstract concepts. In short, mathematics has evolved from a practical tool into a science exploring the universal laws of nature.
Although formal proofs have demonstrated clear advantages in modern mathematical research and shown great potential in enhancing the accuracy and rigor of mathematical studies, their development still faces challenges. The steep learning curve is a primary issue, as formal proofs require expressing complex mathematical concepts in rigorous symbolic and logical language. While this eliminates ambiguity, it can also make mathematical thinking more cumbersome and complex, especially for high-level abstract concepts, where the formalization process may become extremely intricate and lengthy, increasing the difficulty of understanding and communication. Although formal proofs offer higher verifiability, they also mean that every detail must be carefully scrutinized and confirmed, particularly when dealing with complex mathematical structures, requiring researchers to expend extra effort to ensure each step is correct.
Promoting the efficiency and accessibility of formal proof generation and verification is not only an inevitable choice to address the complexity of modern mathematical research and practical application needs but also a crucial means to improve research efficiency, ensure result reliability, and advance educational development. Introducing automation and interactive theorem-proving tools has become a key strategy.
The development of formal proof tools reflects the profound integration of mathematics and computer science. The history of formal proof tools dates back to the mid-20th century, with early automated theorem provers like the Resolution Principle and Herbrand’s Theorem laying the foundation for formal proofs. From the 1970s to the 1980s, formal methods rapidly advanced, and several important theorem-proving tools emerged. For example, tools like Coq (1989) and Isabelle (1986) gained popularity, supporting interactive proofs and allowing users to construct proofs in a more natural way. In the 1990s, rich libraries and tools flourished, with Coq's Mathematical Components library widely used in number theory and algebra, and Isabelle/HOL, combining higher-order logic with interactive proofs, applied in formal verification and security analysis.
From the 2000s to the present, dependent type theory has increasingly been applied in formal proofs. Dependent type theory is a type system that tightly integrates types with values, allowing types to depend on certain values. Through dependent types, formal proofs enable users to define more complex structures and functions, precisely defining mathematical objects and their properties, and expressing intricate logical relationships through types. Additionally, dependent type theory allows type checking at compile time, meaning the correctness of formal proofs can be verified at the code level.
Lean 4's advantages lie in its efficient proof capabilities and robust library support. It supports modular programming, allowing users to organize proofs and definitions into modules for easy reuse and management. Furthermore, Lean 4's interactive proof environment enables users to construct proofs step-by-step and verify their correctness in real-time. However, Lean 4 also faces challenges, such as limited automated reasoning capabilities when handling complex mathematical problems, relying on user-provided hints and structures.
While Lean 4 demonstrates significant strengths in the field of formal proofs, there is still room for improvement in efficiency. First, Lean 4's automated reasoning capabilities remain dependent on user-provided hints and structures when dealing with complex mathematical problems, limiting its level of automation. Although Lean 4 boasts a rich mathematical library, its coverage of knowledge and theorems in specific domains remains incomplete. Certain branches of mathematics or emerging fields may lack sufficient formalization, restricting its automated proof capabilities. This means that when faced with highly complex or non-standard propositions, Lean 4 may struggle to generate effective proofs, requiring more human intervention and guidance.
6. Conclusion
On the path to exploring AI reasoning capabilities, mathematical formal proofs are becoming an increasingly important key. By integrating this concept into the training of large models, we can significantly enhance their reasoning abilities. Abaka AI's high-quality mathematical datasets not only cover a wide range of mathematical branches but also include diverse problem types and advanced logical structures, providing comprehensive learning materials for models. This enables reasoning models to better understand and tackle complex mathematical problems, allowing them to play a greater role across various fields.
